X与Y不相关但在多元回归中系数却显著?

多元线性回归分析是一种应用范围很广的定量预测方法，是使用最多的需求预测方法之一，也是医学领域应用最广泛的建模技术之一。

多元回归分析，又称重回归分析，就是通过多个因素（自变量）对目标（因变量）进行预测的一种手段和方法。多元回归分析，可以理解为有两个或两个以上自变量的回归分析。多元回归分析自变量和因变量的关系，可以多元方程式的形式表现出来，这个多元方程式就是多元回归方程。

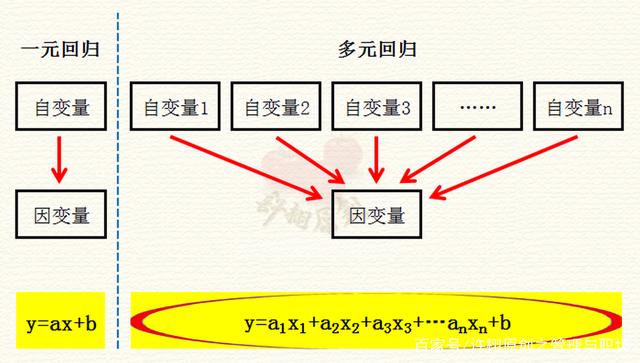
多元回归拥有两个或两个以上的自变量，多元线性回归方程式是y=a1x1+a2x2+…+anxn+b。多元回归方程与一元回归方程很相似，区别在于一元回归方程是一个自变量，而多元回归方程有多个自变量。（见下图）

下图式中，y为因变量，即我们要预测的目标变量，x1为自变量1，x2为自变量2，x3为自变量3，…，xn为自变量n，。

a1、a2、a3、…、an分别为x1、x2、x2、…、xn的回归系数（也叫偏回归系数）,代表每个自变量对因变量影响的程度。

b为截距，为多元线性回归直线与Y轴交点的纵坐标。

纳入多元回归方程自变量的确定。

前文我说到，影响需求的因素，也就是说自变量有很多个，我们不可能也没有必要把这些自变量都纳入多元回归方程。何况这些自变量有的影响大，有的影响小，有的重要，有的不重要。这时，我们需要做出选择，需要采取办法将影响大的自变量纳入多元回归方程。

采取什么方法呢？做相关分析。即对每一个自变量和因变量做相关分析，也就是求出每一个自变量和因变量的相关系数R，然后按一定的标准，将相关系数R达到一定标准的纳入回归方程。

理论上校正了多重共线性以后，具有显著的相关因素才能被纳入线性回归方程。事实上，有时候观察其临床意义，只要有临床意义，哪些可能不相关，也会被纳入线性方程，这时候可能会出现这样的现象：X与结局Y并不相关，但是放在多元回归中，系数却显著，这明显不符合常理，这可能是什么原因呢？

了解这个原因，需要明白几个关键的概念：中介变量(Mediator)，混淆变量(Confounder)，调节变量(Moderator)，暴露变量(Exposure), 协变量(Covariate), 结果变量(Outcome)，对撞变量(Collider)的概念。可以参考：控制变量、调节变量和中介变量的区别与联系

所谓X与结局Y相关，X是Y的独立因素，主要对于“独立”的理解，如果X并不是独立的因素，就可能出现上述样的情况。因为因果理论为两个变量如何无条件独立但有条件地依赖提供了另一种解释。

同时，相关分析与回归分析，表面看来是先后顺序，事实上，底层逻辑有很大不同：

1.在回归分析中，解释变量称为自变量，被解释变量称为因变量，相关分析中，并不区分自变量和因变量，各变量处于平的地位。--（自变量就是自己会变得变量，因变量是因为别人改变的）

2.在相关分析中所涉及的变量全部是随机变量，在回归分析中只有只有因变量是随机变量。

3.相关分析研究主要是为刻画两类变量间的线性相关的密切程度，而回归分析不仅可以揭示自变量对因变量的影响大小，还可以由回归方程进行预测和控制。

因此，自变量与因变量并不是按“理想”的因果，且独立的话，那么就有可能出现上述情况了。下面看三个例子，看看在第三个变量加入进来后两个变量的关系如何发生改变了的。

A. 混杂因素：

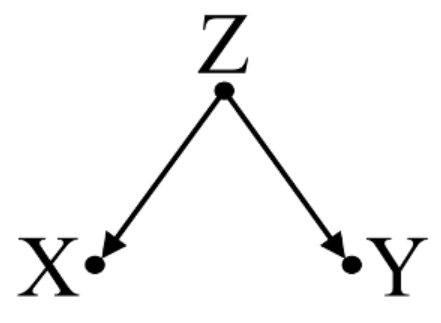
X 和 Y 在双变量回归中相互依赖，但在控制了混杂因素 Z 的多元回归中保持独立。

B. 对撞因素：

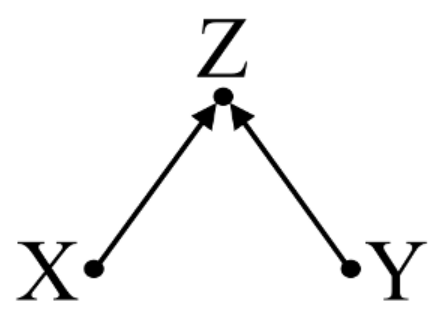
X 和 Y 在双变量回归中相互独立，但在控制了对撞因素 Z 的多变量回归中相互依赖。

C. 偶然取消Incidental cancellation：

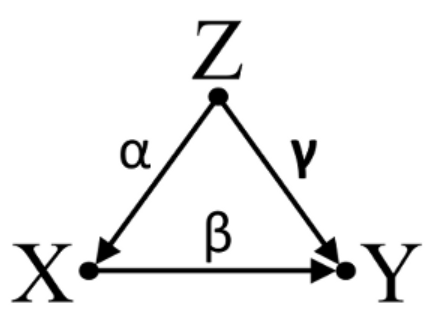
X 和 Y 在双变量回归中相互独立，但在控制了混杂因素 Z 的多变量回归中相互依赖。

如果碰到上述情况，就不能简单利用线性回归了，需要考虑上述复杂因素，解决这些混杂以后，才能再进行分析了。

参考资料：

许栩，需求预测，线性回归分析详解：如何选择自变量及求解多元回归方程

计量经济圈